Exercise 140519

Problem 1

Two coaxial metal pipes of radii $a$ and $b$ ($a<b$) are lowered vertically into a large oil bath. If a voltage $V$ is applied between the pipes, show that the top level of the oil between the pipes rises a height

$H={\frac {V^{2}(\kappa -1)\epsilon _{0}}{\ln(b/a)\rho (b^{2}-a^{2})g}}$

where $\kappa$ is the dielectric constant and $\rho$ is the density of the oil

solution

When equilibrium has been reached the battery can be disconnected without effect, so we consider only work done by the electric force and the gravity.

$\Delta U_{\textrm {grav}}=-\Delta U_{\textrm {el}}$

The center of mass of the displaced oil is at height $H/2$, thus for a small displacement of the top level of the oil $\Delta H$, the work done by gravity is

$\Delta U_{\textrm {grav}}=\Delta (mgH/2)=\pi (b^{2}-a^{2})H\rho g\Delta H$

(assuming the lower level of the oil does not change appreciably).

Since the charge $Q$ on the pipes remains constant, while their capacitance $C$ changes with the presence of oil between them, the work done by the electric force is

$\Delta U_{\textrm {el}}=\Delta (Q^{2}/2C)=-(Q^{2}/2C^{2})\Delta C=-(V^{2}/2)\Delta C$

The capacitance per unit length between coaxial cylindrical conductors with a dielectric between them is

$E={\frac {\lambda }{2\pi \epsilon _{0}R}}$

$V=V_{b}-V_{a}=-\int _{a}^{b}{\vec {E}}.d{\vec {l}}=-{\frac {\lambda }{2\pi \epsilon _{0}}}\int _{R_{1}}^{R_{2}}{\frac {dR}{R}}$ $=-{\frac {\lambda }{2\pi \epsilon _{0}}}\ln(a/b)={\frac {\lambda }{2\pi \epsilon _{0}l}}\ln(b/a)$

$C_{l}={\frac {\lambda }{V}}=2\pi \epsilon _{0}\kappa /\ln(b/a)$

so

$\Delta C=2\pi \epsilon _{0}(\kappa -1)\Delta H/\ln(b/a)$

putting all together:

$\pi (b^{2}-a^{2})H\rho g\Delta H=(V^{2}/2)2\pi \epsilon _{0}(\kappa -1)\Delta H/ln(b/a)$

Problem 2

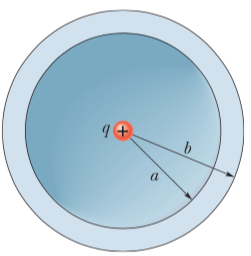
A nonconducting spherical shell of inner radius $a$=2.00 cm and outer radius $b$=2.40 cm has (within its thickness) a positive volume charge density $r=A/r$, where $A$ is a constant and $r$ is the distance from the center of the shell. In addition, a small ball of charge $q$ =45.0 fC is located at that center. What value should $A$ have if the electric field in the shell ($a\leq r\leq b$) is to be uniform?

Solution

Since our system possesses spherical symmetry, to calculate the electric field strength, we may apply Gauss’ law and take the Gaussian surface to be in the form of a sphere of radius $r$

To find an expression for the electric field inside the shell in terms of $A$ and the distance from the center of the shell, choose A so the field does not depend on the distance. We use a Gaussian surface in the form of a sphere with radius $r_{g}$, concentric with the spherical shell and within it ($a<r_{g}<b$). Gauss’ law will be used to find the magnitude of the electric field a distance $r_{g}$ from the shell center. The charge that is both in the shell and within the Gaussian sphere is given by the integral $q_{s}=\int \rho dV$ over the portion of the shell within the Gaussian surface. Since the charge distribution has spherical symmetry, we may take $dV$ to be the volume of a spherical shell with radius rand infinitesimal thickness $dr$: $dV=4\pi r^{2}dr$. Thus,

$q_{s}=4\pi \int _{a}^{r_{g}}\rho r^{2}dr=4\pi \int _{a}^{r_{g}}{\frac {A}{r}}r^{2}dr=4\pi \int _{a}^{r_{g}}rdr=2\pi A(r_{g}^{2}-a^{2})$

The total charge inside the Gaussian surface is

$q_{\textrm {encl}}=q+q_{s}=q+2\pi A(r_{g}^{2}-a^{2})$

The electric field is radial, so the flux through the Gaussian surface is $\Phi =4\pi r_{g}^{2}E$ where E is the magnitude of the field. Gauss’ law yields

$\Phi =q_{\textrm {encl}}/\epsilon _{0}\rightarrow 4\pi \epsilon _{0}Er_{g}^{2}=q+2\pi A(r_{g}^{2}-a^{2})$

$E={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{r_{g}^{2}}}+2\pi A-{\frac {2\pi Aa^{2}}{r_{g}^{2}}}\right]$

For the field to be uniform, the first and last terms in the brackets must cancel. They do if $q-2\pi Aa^{2}=0$ or $A=q/2\pi a^{2}$. With $a=2.00\times 10^{-2}$ m and $q=45.0\times 10^{-15}$ C, we have $A=1.79\times 10^{-11}$ C/m