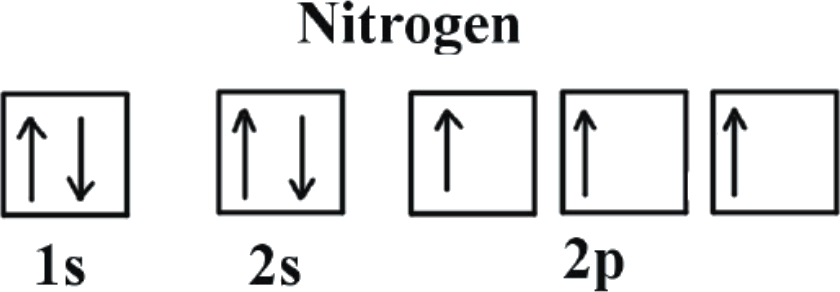
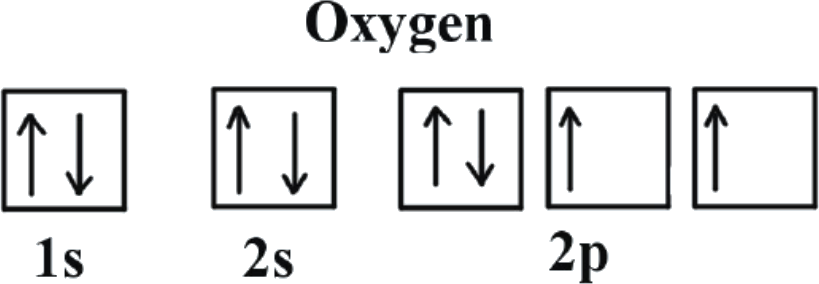
When assigning electrons to orbitals, an electron first seeks to fill all the orbitals with similar energy (also referred to as degenerate orbitals) before pairing with another electron in a half-filled orbital. Atoms at ground states tend to have as many unpaired electrons as possible. In visualizing this process, consider how electrons exhibit the same behavior as the same poles on a magnet would if they came into contact; as the negatively charged electrons fill orbitals, they first try to get as far as possible from each other before having to pair up.

1. For a given electron configuration, the term with maximum multiplicity $2S+1$ or, equivalently, the term with maximum $S$, the spin angular momentum, has the lowest energy.
2. For a given multiplicity, the term with the largest value of $L$ (the orbital angular momentum) has the lowest energy.
3. For a given term, in an atom with the outermost subshell half-filled or less, the level with the lowest value of $J$ (total angular momentum,$\bf{J=L+S}$) lies lowest in energy. If the outermost shell is more than half-filled, the level with the highest value of $J$ is the lowest in energy.

Electrons always enter an empty orbital before they pair up. Electrons are negatively charged and, as a result, they repel each other. Electrons tend to minimize repulsion by occupying their own orbitals, rather than sharing an orbital with another electron. Furthermore, quantum-mechanical calculations have shown that the electrons in singly occupied orbitals are less effectively screened or shielded from the nucleus. Unpaired electrons in singly occupied orbitals have the same spins. Technically speaking, the first electron in a sublevel could be either "spin-up" or "spin-down." Once the spin of the first electron in a sublevel is chosen, however, the spins of all of the other electrons in that sublevel depend on that first spin. As a convention, the first electron, and any other unpaired electron, is labeled as "spin-up."

The third one is the extension of one and two to $LS$-coupling regime. $\bf{J=L+S}$ where $\bf{S}$ is the total spin angular moment $\bf{S}=\sum_i \bf{s}_i$ and $\bf{L}$ is the total orbital angular moment $\bf{L}=\sum_i \bf{l}_i$ ($bf{s}_i$ and $bf{l}_i$ are spin and orbital momenta of electrons) 

References:

chem.libretexts
postnikov lecture