Let's start our analysis using the collinear picture (also called conventional picture) where all magnetic moments are parallel (or antiparallel) to each other. This practically means we are ignoring the spin-orbit coupling (and even consequently relativistic effects to a degree). In many high-symmetry crystalline systems, the orbital moment isquenched, and can be safely neglected. This is not always the case. For example in a number of FCC antiferromagnetic materials.
In collinear picture, multiple magnetic solutions are allowed, i.e. although $N_\uparrow+N_\downarrow$ is constant and predetermined, $N_\uparrow-N_\downarrow$ can vary. A typical example is the high spin and low spin states of Fe.
Isolated atom or ion
Orbital magnetic moment of an electron in an isolated atom or ion:
$$\begin{aligned} \vec{\mu} &= \frac{-e}{2m_e}\vec{L} \\ \mu&=-\frac{e\hbar}{2m_e}\sqrt{l(l+1)}\\ \mu_z^\text{orb}&=-m_l\mu_\text B\\ \mu_\text B&=\frac{e\hbar}{2m_e} \end{aligned}$$
Spin magnetic moment of an electron in an isolated atom or ion:
$$\begin{aligned} s &= \frac{1}{2} \\ m_s&=\pm\frac{1}{2}\\ \mu_z^\text{spin}&=\pm g \mu_\text B\end{aligned}$$
notice that $ g\approx 2$ hence $\mu_z^\text{spin}$ is NOT $\frac{1}{2}\mu_\text B$
Total orbital and spin magnetic moments of an isolated atom or ion:
$$\begin{aligned}\mu_z^\text{orb}&=\sum_{\text{occ.}\alpha}\sum_{\uparrow,\downarrow}(-m_\alpha)\\\mu_z^\text{spin}&=\sum_{\text{occ.}\alpha}\left(n_\uparrow - n_\downarrow\right)\end{aligned}$$
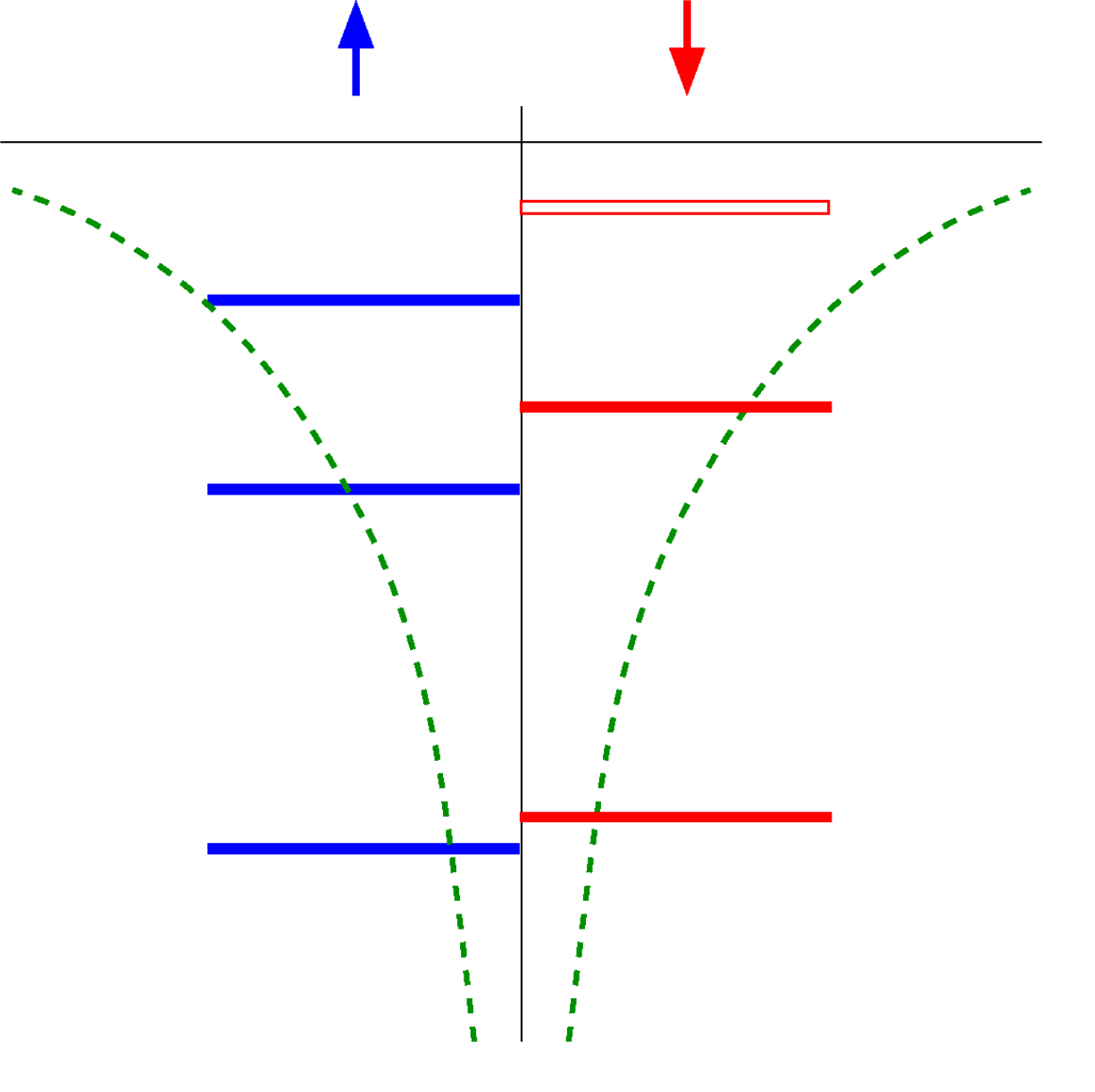
From the Atom to the Cluster (molecule) then to the Condensed matter
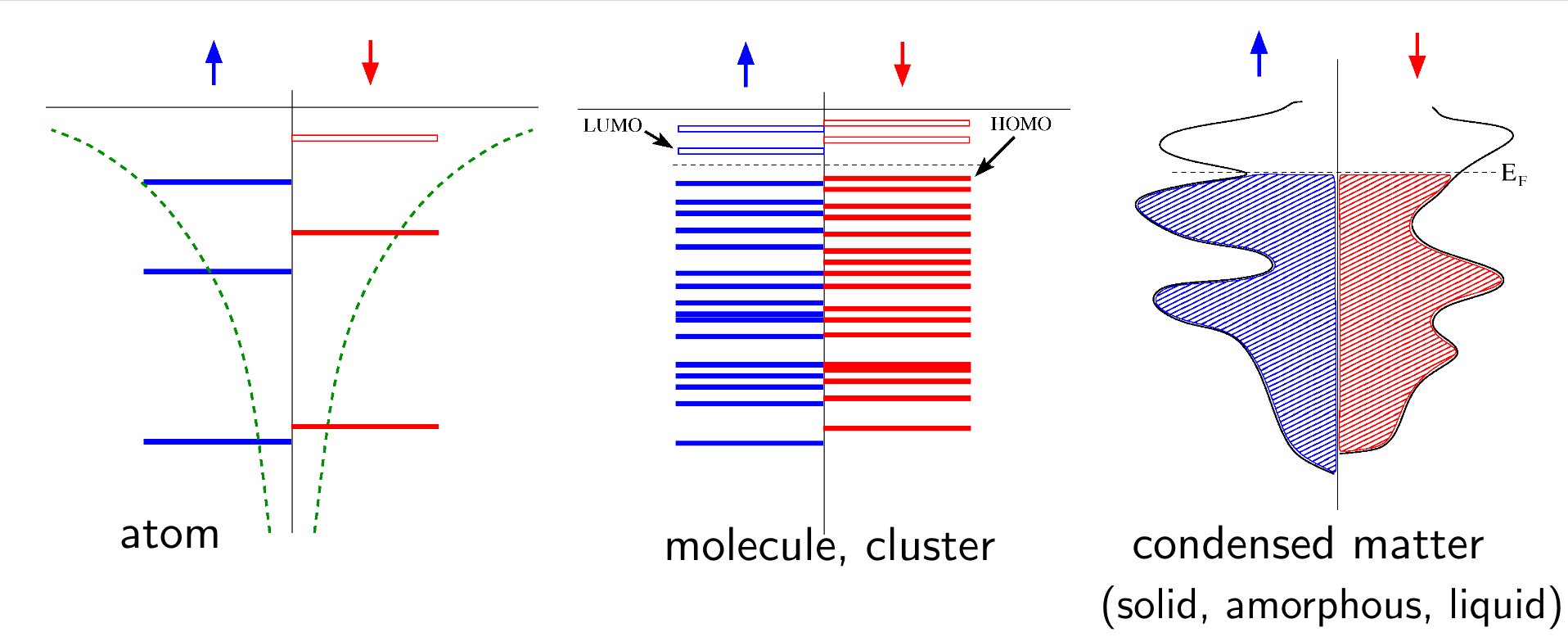
As the number of atoms in the system increase, the discrete energy levels evolve into a distribution called density of states (DOS). In an atomic and molecular systems, number of spin up electrons $N_\uparrow$ and number of spin down electrons $N_\downarrow$ are integer numbers. So are the number of partially occupied bands $Q=N_\uparrow+N_\downarrow$ and the total magnetization $M=N_\uparrow-N_\downarrow$. In condensed matter systems, the number of partially occupied bands $Q$ is still an integer, however there is no a priori restriction on $M$ per unit cell being integer.
Some material types according to their magnetism
Ferromagnetic
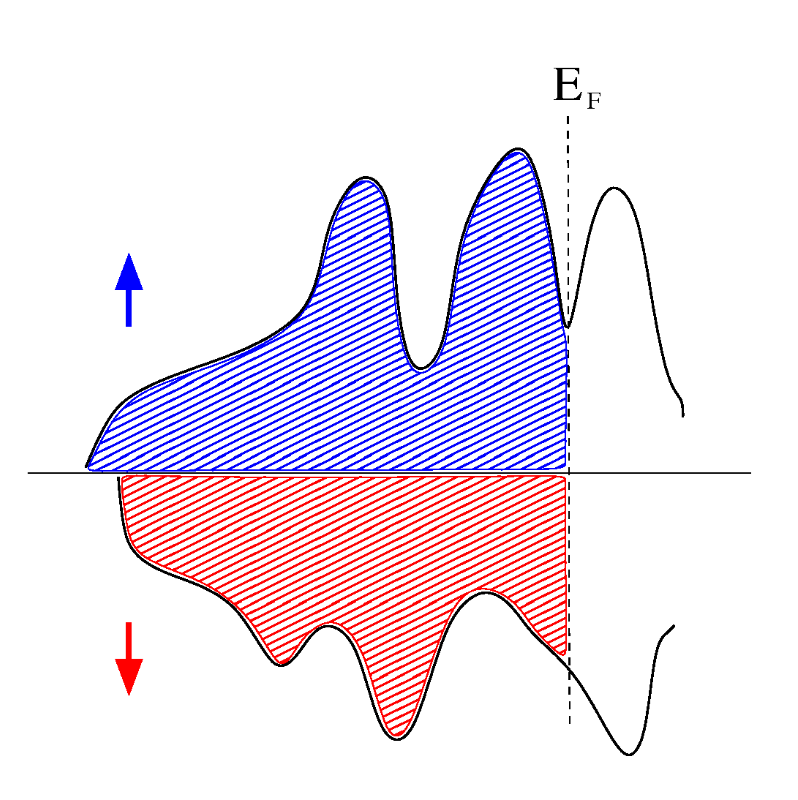
Ferromagnetic materials possess a permanent magnetic moment in the absence of an external field and exhibit very large, permanent magnetizations. The spontaneous magnetization is not apparent in materials which have not been exposed to an external field, because of the presence of domains in the material each having its own direction of magnetization. When a field is applied, the domains in which the magnetization is more nearly parallel to the field grow at the expense of the domains with less favorable alignments. When the applied field is removed, a part of the induced domain alignment may be preserved so that the body acts as a permanent magnet. Spontaneous magnetization is due to the alignment of uncompensated electron spins by the strong quantum-mechanical “exchange” force.
Antiferromagnetic
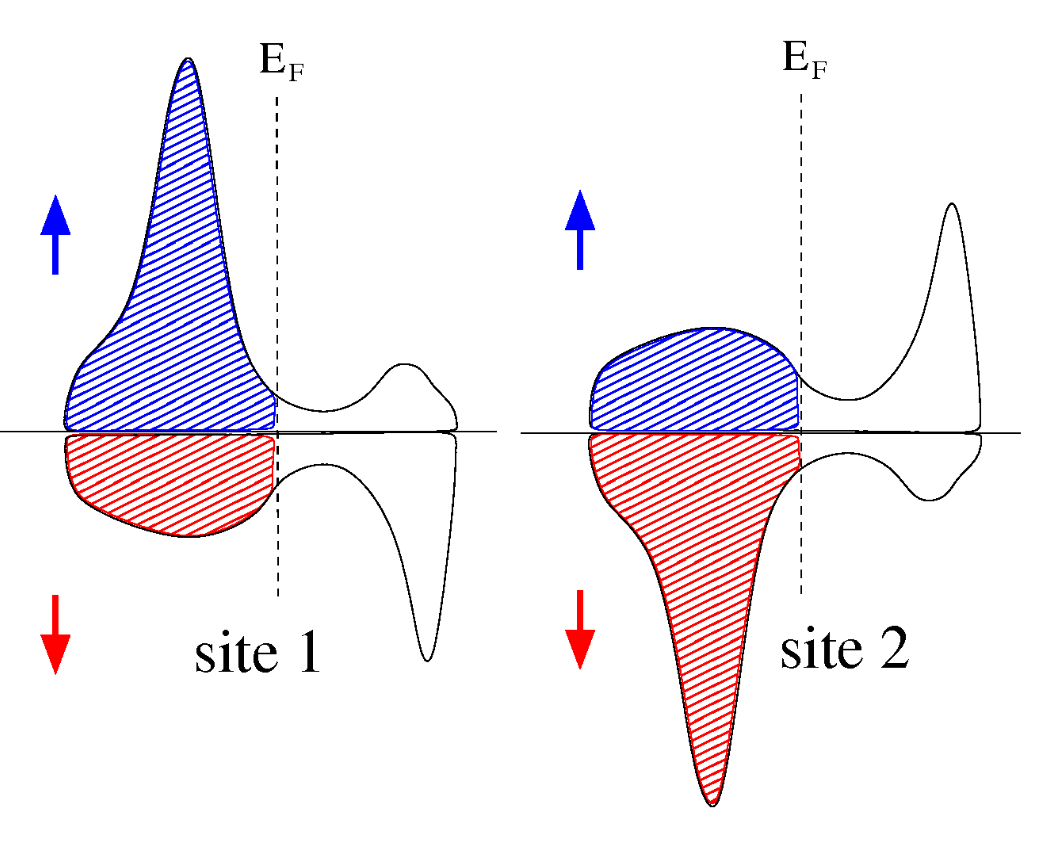
In materials that exhibit antiferromagnetism, the local magnetic moments, align in a regular pattern with neighboring spins (on different sublattices) pointing in opposite directions. Hence we need to label two local sites, 1 and 2. By definition, the total magnetisation in the magnetic primitive cell is zero, $M_\text{tot}=M_1+M_2=0$
The magnetisation in the local sites $M_1$ and $M_2$ are definition dependent and not necessarily integers!. The criteria they must obey is $M_1=-M_2$, and $N_1^\uparrow=N_2^\downarrow$; $N_1^\downarrow=N_2^\uparrow$
Dielectric
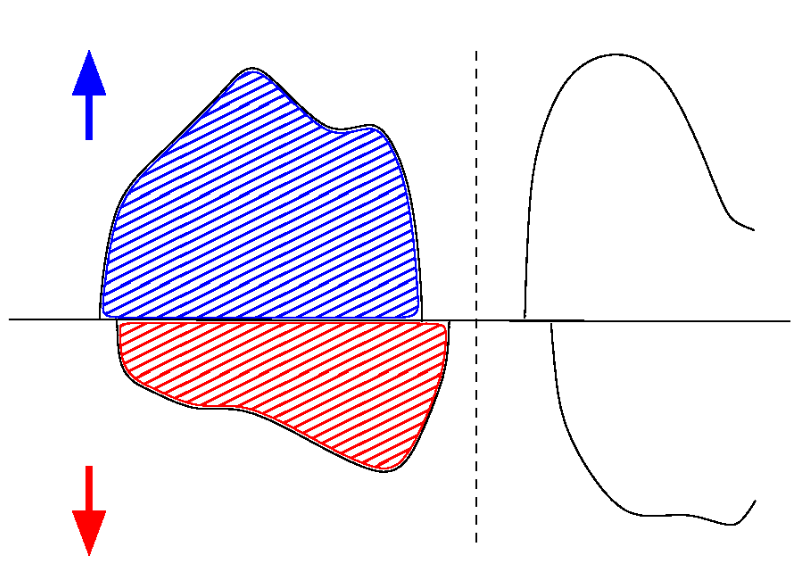
In the dielectric case, the number of occupied bands, $Q=N_\uparrow+N_\downarrow$ is an integer. Hence $M_\text{tot}$ is also an integer. However, since the local magnetic moment depends on how you define what "local" is, $M_\text{loc}$ is definition dependent.
Semimetal
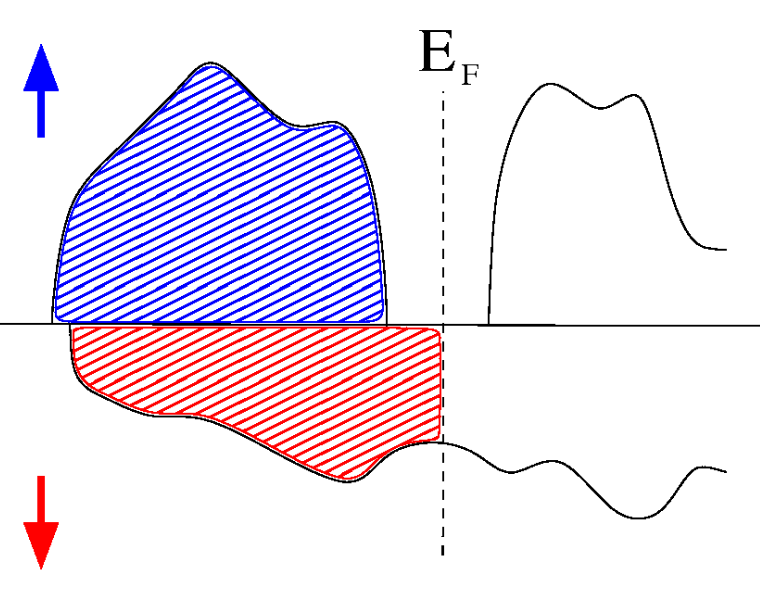
In a semimetal, although there is a band gap in one of the spin channels (e.g.: $N_\uparrow$), the other channel crosses $E_\text F$, as in a metal. $Q=N_\uparrow+N_\downarrow$ is an integer, $N_\uparrow$ is an integer, so $N_\downarrow$ must also be an integer. This means $M=N_\uparrow-N_\downarrow$ is an integer.
On calculating "local" quantities.
Mulliken analysis for obtaining localised quantities depend on the choice of basis functions and thus they are not uniquely defined. Using real space (spatial) charge/spin density ($\rho$) is basis set independent. One can write a “transferable”(albeit obviously not unique) “definition” of local magnetic moment
$$m_{\text{atom},\alpha}=\int_{\Omega \text{around }\alpha}d\mathbf{r}\left[\rho^\uparrow(\mathbf r)-\rho^\downarrow(\mathbf r)\right]$$
Then the question is how to determine "around atomic centre $\alpha$". You can use muffin tin spheres of a given radius, or use Bader basins.